目標
帰無仮説について理解する
対立仮説について理解する
有意水準について理解する
P値について理解する
z検定について理解する
帰無仮説と対立仮説
帰無仮説とは
帰無仮説（H₀）とは、統計的検定でまず前提とする「効果がない／差がない」という基準の仮説です。データがこの仮説と矛盾するほど、極端であれば、H₀を棄却（効果があるとする／差があるとする）します。
対立仮説とは
対立仮説（H₁ / H_A）とは、統計的検定で「効果がある／差がある」と主張する仮説です。基準となる帰無仮説（H₀：効果なし／差なし）に反する内容で、データが十分にH₀と矛盾すると判断できたとき、H₀を棄却しH₁を支持します。
判断基準
- 判断基準は「有意水準 α（一般には 5% や 1%）」です。
- P値 ≤ α → H₀を棄却（統計的に有意）
- P値 > α → H₀は棄却できない（＝有意差は示せない）
- コインの公平性
- H₀: 表の確率 p = 0.5
- H₁: p ≠ 0.5（両側）
- A/Bテスト（CVRの比較）
- H₀: pA = pB（＝差 0）
- H₁: pB > pA（片側、Bの改善だけ主張）
- 平均の差（薬効）
- H₀: μ治療 − μ対照 = 0
- H₁: ≠ 0（両側）または > 0（片側）
- 回帰係数
- H₀: 係数β = 0（説明変数の効果なし）
- RDD（回帰不連続）
- H₀: カットオフでの“ジャンプ” = 0（処置効果なし）
- 合成コントロール
- H₀: 介入後も実測＝合成（ギャップの平均 0）
P値・有意水準・帰無/対立仮説を使った練習
「ある地域の、ある国道では、雨の日に限って渋滞が発生するという住民の声から、それが、本当に正しいのかをデータをもって確認する」ということを例に、P値・有意水準・帰無/対立仮説を使った練習を行います。
有意水準（α）とは
「帰無仮説（H₀）が本当なのに、まちがって棄却してしまう確率の上限」としてあらかじめ決めておく基準です。典型的には 5%（0.05） や 1%（0.01） が使われます。P値 ≤ α なら H₀を棄却（統計的に有意）、P値 > α なら 棄却できない（＝有意差を示す証拠が不足）とします。
P値 とは
帰無仮説（H₀）が正しいと仮定したとき、観測した統計量と同じかそれ以上に「極端な結果が出る確率」です。
- 両側検定：正負どちら側でも「これ以上」
- 片側検定：指定した方向に「これ以上」
設計（例）
帰無仮説 H₀：「雨でも渋滞は増えない」
例：雨と晴れで平均速度は同じ（μ_rain = μ_clear）／渋滞率は同じ（p_rain = p_clear）
対立仮説 H₁：「雨で渋滞が増える」
例：平均速度が下がる（μ_rain < μ_clear）／渋滞率が上がる（p_rain > p_clear）
有意水準 α：5% を目安に
サンプルデータ（架空例）と その分析
6月1日から10日の期間で、一時間ごとのデータを取得。データには「曜日」「雨かそうでないかを 0/1 で判定」」「雨量をmm単位で」「気温」「事故の有無」「車の速度」などを取得。
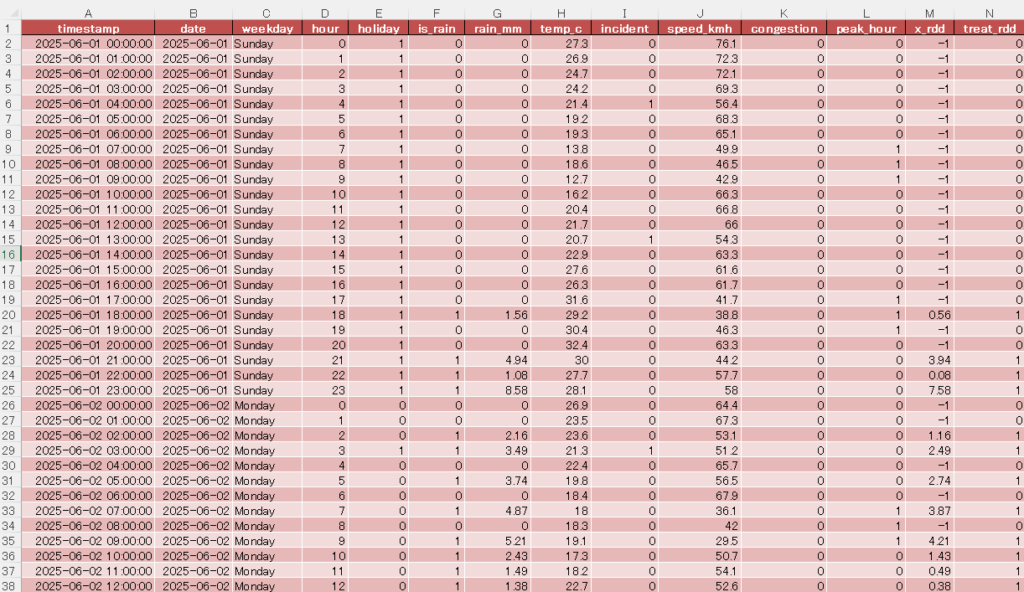
雨 vs 晴れの「平均速度」の差（t検定・片側）
is_rain=1とis_rain=0でspeed_kmhの平均を出力します。
- 「is_rain=0の平均速度」=AVERAGEIF($F$2:$F$241,0,$J$2:$J$241)
- is_rain=0の平均速度 58.07253521
- 「is_rain=1の平均速度」=AVERAGEIF($F$2:$F$241,1,$J$2:$J$241)
- is_rain=1の平均速度 48.58571429
- 「P値」= T.TEST(FILTER(J2:J241, F2:F241=1),FILTER(J2:J241, F2:F241=0),1,3)
- P値 0.00000000002
雨 vs 晴れの「渋滞率」の差（2標本比率のz検定・片側）
ピボットで 雨/晴れ(0/1) × 渋滞(0/1) の件数を集計します。
- 渋滞件数：
- x_clear = 0（晴れで渋滞=1 の件数：ピポットテーブルでは空欄）
- x_rain = 3（雨で渋滞=1 の件数）
- n_clear（行の総計） = 142（is_rain=0 の総観測数）
- n_rain（行の総計） = 95（is_rain=1 の総観測数）
z検定とプール比率とは？
z検定は、「たまたま？ ほんとう？」を調べる方法です。手順は次の通りです。
- まず約束（考えの出発点）を決める
→「晴れでも、雨でも、渋滞の起きやすさは同じ」と考える（帰無仮説）。 - 実際の数を見て、どのくらい、回数が違うかをはかる
→ 差が大きいほど、「同じはず」では説明しにくい。 - その差が起きる確率（P値）がとっても小さければ、
「たまたまじゃなさそう＝雨の日は本当に混みやすいのかも」と考る。
たとえば：コインを100回投げて表が70回。
「半分のはず（50回）」という約束の下では、70回は回数が多い。
これが z検定の考え方。
プール比率は、「全部をまとめた割合」のことです。例えば、「晴れ」と「雨」を同じと考えるなら、2つをいったん合体して、全体での“渋滞の割合”を数えることができます。
- 例：晴れで渋滞3回/100回、雨で渋滞5回/100回なら、
プール比率 ＝ (3＋5) ÷ (100＋100) ＝ 8/200＝0.04（4%）。
これを「同じはず」の基準の割合（＝プール比率）として使います。
どうしてまとめるのか？：出発点が「同じ」と考えるから、2つをひとつの袋に混ぜて、「ふつうはこのくらい起きる」を見積もります。
プール比率の式：
帰無仮説 H₀:𝑝1=𝑝2のもとで、2群に共通と仮定した比率の最尤推定値
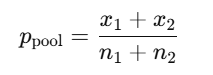
- プール比率：
- p = (x_rain + x_clear) / (n_rain + n_clear)
- p = ( 3 + 0 ) / ( 142 + 95 )
- p = 0.012658228
- 標準誤差：
- SE = SQRT(p*(1-p)*(1/n_rain + 1/n_clear))
- SE = SQRT(0.0125*(1-0.0125)*(1/142 + 1/95))
- SE = 0.01481796
標準誤差とは？
- たとえば、「日本人の平均身長」を知りたいとします。
- でも全員を測れないので、ある程度の規模の人数の身長から平均を出します。
- すると、その平均は本来の平均とは少しズレます。
- 標準誤差は、この「平均のズレの大きさ」を表すものです。
→ つまり、「今回の平均はどれくらい不確か（ふらつく）か」の目安です。
※データ数が増えると標準誤差は小さくなります（平均が安定）
標準誤差の式：（nはサンプル数）
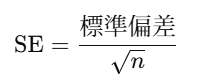
- 統計量（z 近似）：
- z = (x_rain/n_rain – x_clear/n_clear) / SE
- z = (3 / 142 – 0 / 95) / 0.01481796
- z = 1.42575368295639
z 近似は次の式で表せます。
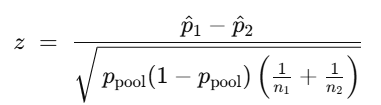
- 片側P値：
- P =1 – NORM.S.DIST(z, TRUE)
- P = 1 – NORM.S.DIST(1.42575368295639, TRUE)
- P = 0.0769697273720911
期待成功数とは？
検定の帰無仮説のもとで「成功（=1）」が何回くらい起きるはずかを表す「期待」の回数です。今回の例で「成功」は 渋滞=1 のことです。
求め方は 2通り あります。
1) 2群比率の z 検定の考え方
帰無仮説 H₀:prain=pclear のもとで共通の確率を「プール比率」として推定し、各群の期待成功率は次の式で表せます。
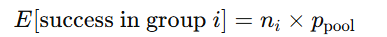
今回の場合は
- 晴れ：142 × 0.012658228 = 1.79746835443038
- 雨：95 × 0.012658228 = 1.40770616798226
2) 2×2表のカイ二乗検定の式
行合計×列合計÷総計 で各セルの期待度数を出します。
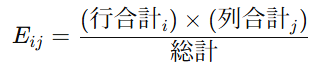
期待成功数：晴れ 1.79746835443038、雨 1.40770616798226 （どちらも <5）
z=1.42575368295639、SE=0.01481796 なので
p^雨−p^晴 = 1.42575368295639 × 0.01481796 ≈ 0.0211
→ 約 2.1 パーセント雨の方が渋滞率は高い
ここまでの解釈
雨の渋滞率は晴れより約2.1ポイント高い傾向がみられた。z近似の片側P=0.077で、5%水準では有意差は確認できず、10%水準では有意。ただし期待度数が小さく近似の信頼性が低いため、Fisherの正確検定での再確認と追加データの収集が望まれる。
→ 期待度数が小さいため、z 近似は過信できないのが現状です。この場合はFisherの正確検定（または二項検定）を優先するのが丁寧です。
Fisherの正確検定：
= 1 – HYPGEOM.DIST(3-1, 98, 3, 240, TRUE)
＝ 0.066847157272951
ここまでの解釈
雨の渋滞率は晴れより高い傾向（差は数ポイント）を示したが、Fisher の正確検定（片側）では P=0.0669。5%水準では有意差は確認できない（10%水準では有意）。件数が少なく推定の不確かさが大きいため、追加データの収集およびピーク時間帯・事故の有無などでの層別やロジスティック回帰による検証を推奨する。
今回は以上となります。（以後の解析は割愛）
Excelでの表示例
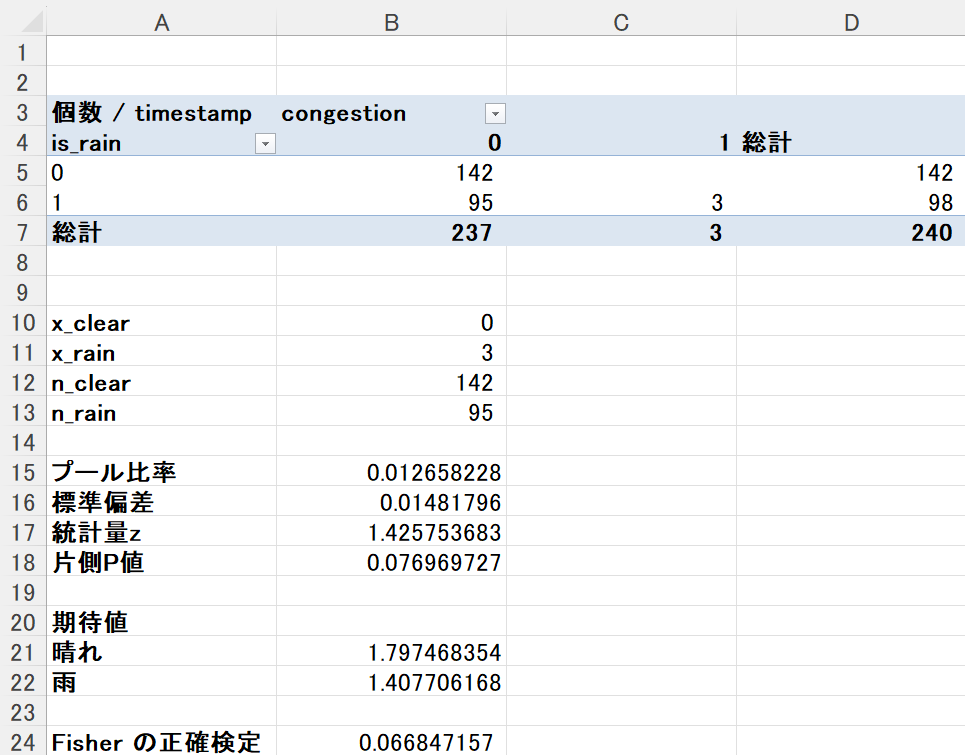
ブックマークのすすめ
「ほわほわぶろぐ」を常に検索するのが面倒だという方はブックマークをお勧めします。ブックマークの設定は別記事にて掲載しています。
