目標
合成コントロール法（Synthetic Control Method）について理解する
合成コントロール法
合成コントロール法は、因果推論の手法のひとつで、政策や介入（イベント）の効果を評価するために用いられます。特に「処置を受けたのが1つのグループ（または地域・国）だけ」の場合に有効です。
ポイントは、処置を受けなかった他のグループ（対照群）を 「加重平均で組み合わせて、似たような『合成グループ』を作る」 ことです。その「合成グループ」の推移を 処置がなかった場合の反実仮想（カウンターファクト）」 とみなし、処置後の差分を「政策効果」として解釈します。
例）ある県で禁煙条例を導入した、その効果を測りたい。
分析の流れ
- 処置群（Treatment Unit）：介入を受けた対象（例：条例を導入した県）
- ドナー群（Donor Pool）：介入を受けなかった他の対象（例：導入していない他県）
- 重み付け：ドナー群をうまく組み合わせ、処置群の「介入前の推移」にできるだけ近づける
- 効果推定：介入後に処置群と合成コントロールの差があれば、それを政策効果と解釈する
合成コントロール法の実施例
サンプルデータ（架空例）
「ある県（処置群A）」で 2015年に禁煙条例を導入したとする例です。
比較対象は「県B」「県C」「県D」。アウトカムは「喫煙率(%)」です。
| 年度 | 処置群A | 県B | 県C | 県D |
|---|---|---|---|---|
| 2010 | 25 | 26 | 24 | 23 |
| 2011 | 24 | 25 | 23 | 23 |
| 2012 | 23 | 24 | 23 | 22 |
| 2013 | 22 | 24 | 22 | 21 |
| 2014 | 21 | 23 | 22 | 21 |
| 2015:条例導入 | 19 | 23 | 22 | 21 |
| 2016 | 17 | 23 | 22 | 21 |
| 2017 | 15 | 22 | 22 | 20 |
| 2018 | 14 | 22 | 21 | 20 |
合成コントロールの重み付け（w）
Solver（ソルバー）で「二乗誤差の最小化」の処理を行います。
（１）「県Bの重み」「県Cの重み」「県Dの重み」を設定する
- 重みの値は任意ですが、設定は合計が「1」となるように設定します。
- 「県Bの重み」+「県Cの重み」+「県Dの重み」= 1
- ※ 例えば、「県Bの重み」=0.4、「県Cの重み」= 0.4、「県Dの重み」=0.2
- ※ 合計が「0」（例えば、「県Bの重み」=0、「県Cの重み」= 0、「県Dの重み」=0だとエラーとなることがあります。）
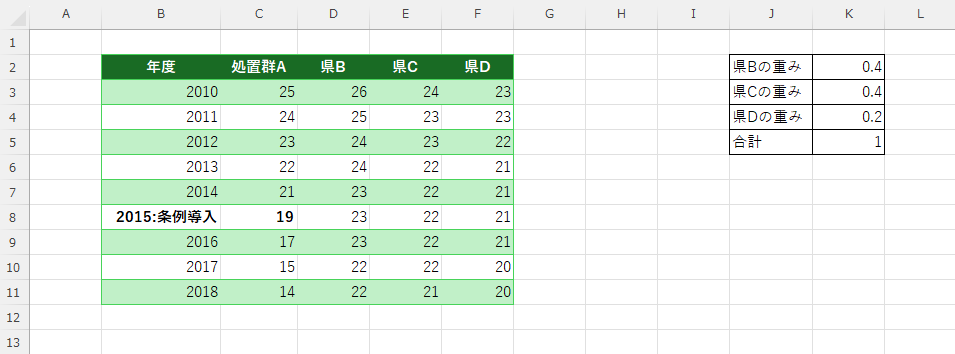
（２）合成コントロールの列を作成して計算式をセルへ追加し、全行へセルをコピーします。
セルG1=D3*$K$2 + E3*$K$3 + F3*$K$4
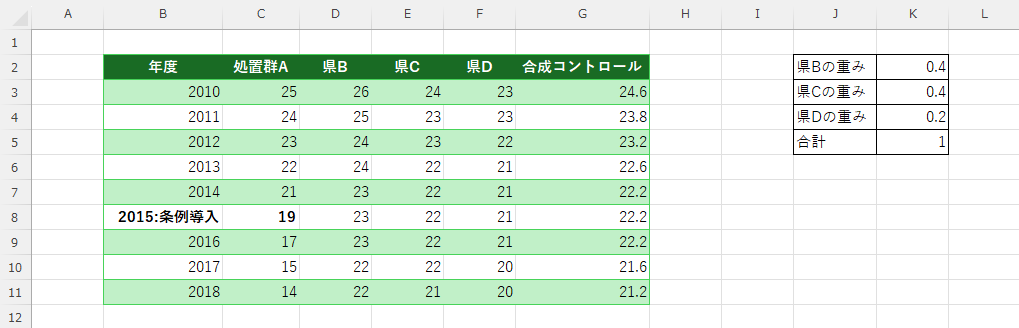
（３）誤差（残差）の列を作成して計算式をセルへ追加し、全行へセルをコピーします。
H列に残差（処置−合成）を置く：セルH3 = SUM(C3-G3)
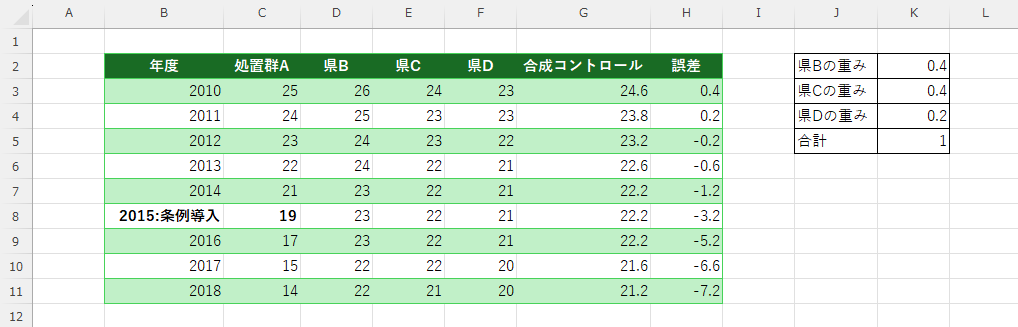
（４）目的関数（SSE）を作成します。計算に利用するセルは介入前の年の誤差までです。
下の式は各セルを二乗して合計を算出しています。
セルK7 = SUMPRODUCT(H3:H7, H3:H7)
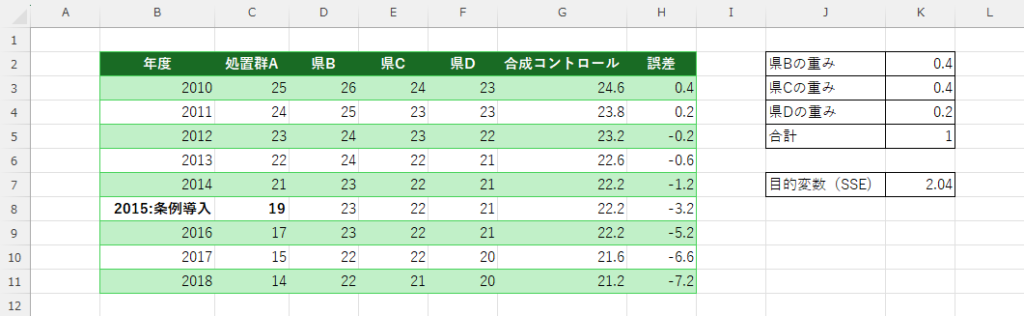
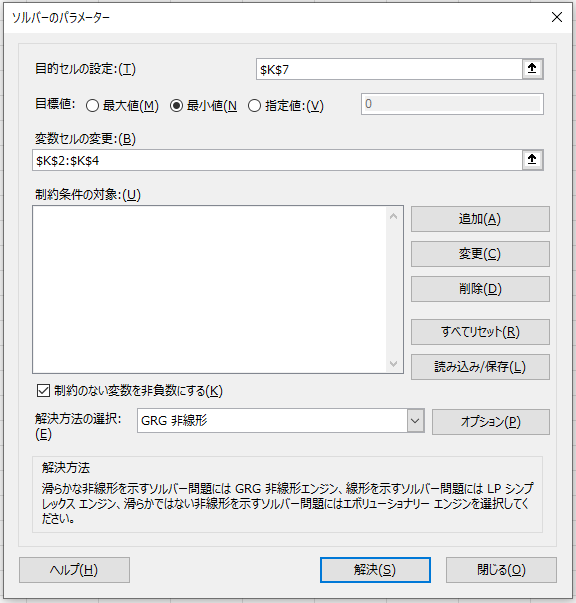
（５）Solver の設定
- 目的セル：$K$7（SSE）を 最小化
- 変数セル：$K$2:$K$4
- 制約：
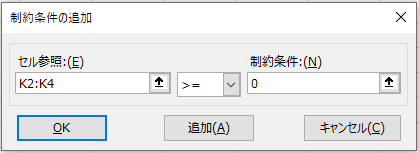
- K2:K4 >= 0（非負制約）
- K5 = 1（重みの合計が1）
- 解法は「GRG 非線形」または「単体法（シンプレックスLP）」を選択します。
- 「解く」をクリックして実行 → 最適な w が得られます。
データタブ→分析から「ソルバー」をクリックします。
制約は右の追加ボタンから追加します。
設定が複数ある場合は条件入力後追加をクリックします。
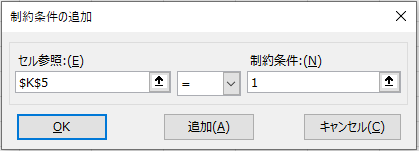
完了したら制約条件の追加ボックスの「OK」をクリックします。
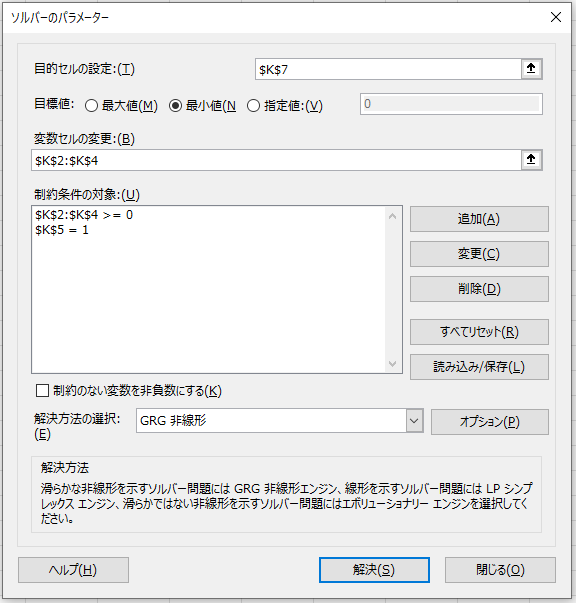
「解決」を実行します。
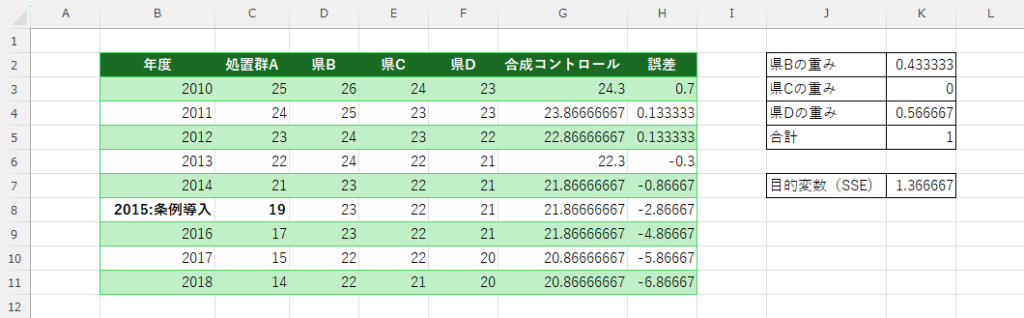
出力結果
県Bの重み 0.433333333
県Cの重み 0
県Dの重み 0.566666667
合計 1
目的変数（SSE) 1.366666667
出力結果とその解釈
出力結果：
重みの意味：県B=0.4333、県C=0、県D=0.5667
介入前（2010–2014）の県Aの推移は、BとDの加重平均で最もよく再現でき、Cは不要だった（重み0）と解釈できます。
前処置期の適合度：SSE=1.3667（5年分）。RMSPE ≈ √(1.3667/5) ≈ 0.52ポイント
尺度（喫煙率20％前後）に対して十分小さめ＝良好なフィットと判断できます。
→ 介入後に大きな乖離が出れば、それを政策効果と解釈しやすい状態。
介入後の推定効果（A−合成）
同じ重みで2015年以降の「合成コントロール」を作ると次のようになります。
| 年 | A（実測） | 合成 | 効果 = A−合成 |
|---|---|---|---|
| 2015 | 19.00 | 21.87 | -2.87 |
| 2016 | 17.00 | 21.87 | -4.87 |
| 2017 | 15.00 | 20.87 | -5.87 |
| 2018 | 14.00 | 20.87 | -6.87 |
負の値は「実測が合成より低い」＝条例導入で喫煙率が下がったことを示唆。しかも年を追って効果が拡大しており、定着・累積効果の可能性があります。
折れ線グラフで可視化（二種類作成）
折れ線（A と 合成）＋介入時点
目的：介入前の一致と介入後の乖離を直感で見せる。
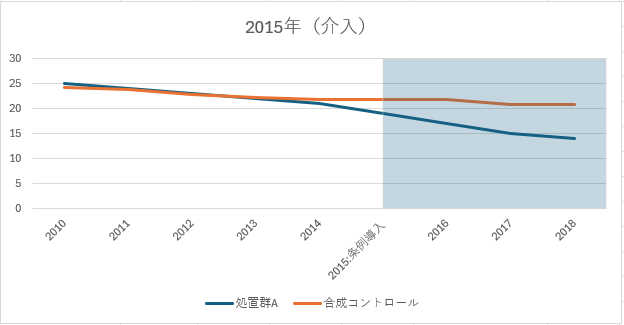
表示要素とポイント
- 折れ線：A、合成コントロールの「2本」です。
- 介入年以降の期間に薄い網掛けをします。
- 凡例は上側、タイトルに「2015年（介入）」を明記します。
折れ線（ギャップ＝A－合成）
目的：効果の符号と、その大きさを一目で伝える。
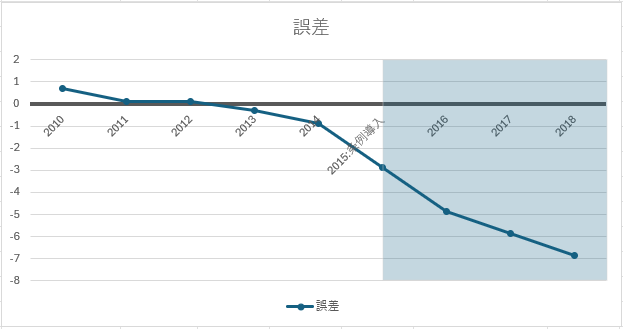
表示要素とポイント
- 0の基準線を太めに
- 介入年以降の期間に薄い網掛けをします。
- 介入前はギャップが0付近で小さいこと、介入後に大きく離れることが分かる配置。
今回は以上となります。
ブックマークのすすめ
「ほわほわぶろぐ」を常に検索するのが面倒だという方はブックマークをお勧めします。ブックマークの設定は別記事にて掲載しています。
