目標
回帰不連続デザインについて理解する
回帰不連続デザイン
回帰不連続デザインは、ある基準値(カットオフ)を境にして、介入を行い、基準値付近の平均の違いを「処理の効果」と解釈する方法です。
基準値付近の平均を利用する理由は、その付近では、処置以外の要因はほぼ同じ(大きな要因とならない)とみなせるからです。そのため、カットオフ前後でアウトカムの平均がどのくらいジャンプ(不連続)するかを見て、それを「処置の効果」と解釈します。
例)テストで50点以上なら奨学金あり、未満なら無しとしたとき、49点と50点の学生は、学力や家庭環境などほぼ同じなのに、進学率に影響がでる。
ポイント整理
- 制度のルール:「50点以上なら奨学金あり」「未満なら無し」
- 観察される現象:
- 49点と50点の学生は、点数の差はわずか1点。
- 学力や家庭環境などの背景要因はほぼ同じと考えられる。
- しかし、制度上は「奨学金なし」と「奨学金あり」に分かれる。
- 因果推論の考え方:
- 進学率に差が見られた場合、その差は「奨学金があるかないか」という処置の効果によるものと解釈できる。
回帰不連続デザインの実施例
サンプルデータ(架空例)
- 処置ルール:
- 得点が50点以上なら奨学金あり(T=1)
- それ未満はなし(T=0)
- 進学率の設定
- 奨学金なし(T=0):進学率 約**%
- 奨学金あり(T=1):進学率 約**%
| ID | 得点 (X) | 奨学金 (T) | 大学進学 (Y) |
|---|---|---|---|
| 1 | 41 | 0 | 0 |
| 2 | 37 | 0 | 0 |
| 3 | 55 | 1 | 1 |
| 4 | 62 | 1 | 1 |
| 5 | 49 | 0 | 0 |
| 6 | 53 | 1 | 1 |
| 7 | 47 | 0 | 1 |
| 8 | 58 | 1 | 1 |
| 9 | 45 | 0 | 0 |
| 10 | 51 | 1 | 1 |
| 11 | 60 | 1 | 1 |
| 12 | 39 | 0 | 0 |
| 13 | 42 | 0 | 0 |
| 14 | 64 | 1 | 1 |
| 15 | 46 | 0 | 0 |
| 16 | 52 | 1 | 1 |
| 17 | 56 | 1 | 1 |
| 18 | 40 | 0 | 0 |
| 19 | 61 | 1 | 1 |
| 20 | 44 | 0 | 1 |
| 21 | 43 | 0 | 0 |
| 22 | 48 | 0 | 0 |
| 23 | 59 | 1 | 1 |
| 24 | 50 | 1 | 1 |
| 25 | 54 | 1 | 1 |
| 26 | 38 | 0 | 0 |
| 27 | 36 | 0 | 0 |
| 28 | 63 | 1 | 1 |
| 29 | 57 | 1 | 1 |
| 30 | 35 | 0 | 0 |
| 31 | 66 | 1 | 1 |
| 32 | 41 | 0 | 0 |
| 33 | 65 | 1 | 1 |
| 34 | 52 | 1 | 1 |
| 35 | 46 | 0 | 0 |
| 36 | 34 | 0 | 0 |
| 37 | 55 | 1 | 1 |
| 38 | 48 | 0 | 0 |
| 39 | 60 | 1 | 1 |
| 40 | 62 | 1 | 1 |
| 41 | 39 | 0 | 0 |
| 42 | 44 | 0 | 0 |
| 43 | 51 | 1 | 1 |
| 44 | 67 | 1 | 1 |
| 45 | 53 | 1 | 1 |
| 46 | 47 | 0 | 1 |
| 47 | 58 | 1 | 1 |
| 48 | 49 | 0 | 0 |
| 49 | 59 | 1 | 1 |
| 50 | 42 | 0 | 0 |
Excelでの手順
- 「奨学金ありグループ」と「なしグループ」に分ける
- 平均値を求める(=AVERAGEIF)
- 奨学金なしの進学率(平均Y)
- 奨学金ありの進学率(平均Y)
- 奨学金の効果(推定値)= 奨学金ありの進学率(平均Y)– 奨学金なしの進学率(平均Y)
- 散布図を作成し、「得点X」を横軸、「進学率Y」を縦軸にプロット
- 50 点を境に進学率がジャンプしていれば、処置効果が視覚的に確認できる
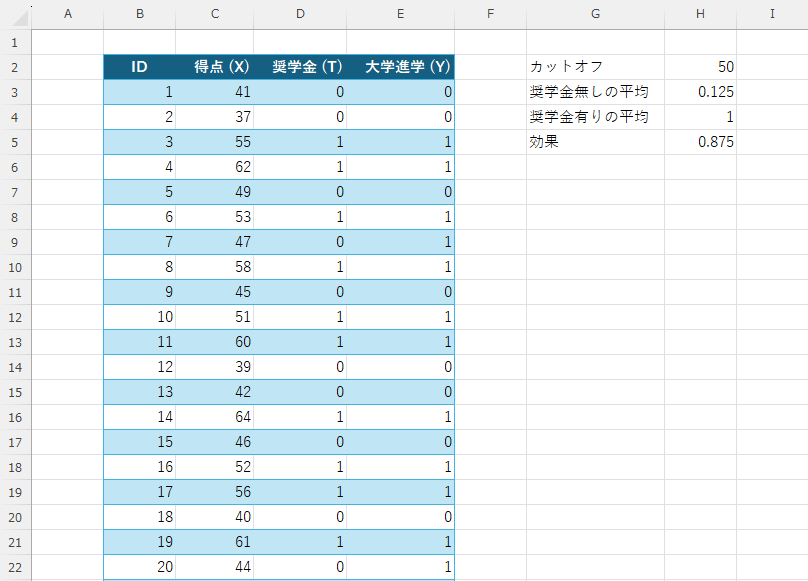
- (奨学金無しの平均)セルH3=AVERAGEIF($D$3:$D$52,0,$E$3:$E$52)
- (奨学金有りの平均)セルH4=AVERAGEIF($D$3:$D$52,1,$E$3:$E$52)
- (効果)セルH5=SUM(H4-H3)
出力結果とその解釈
出力結果:
カットオフ
ルールとして「50点以上なら奨学金あり、未満ならなし」 → カットオフ=50
奨学金無し(T=0)の平均進学率 = 0.125
つまり「奨学金がない学生のうち、12.5%が進学した」
奨学金あり(T=1)の平均進学率 = 1.0
つまり「奨学金がある学生は、ほぼ全員(100%)進学した」
処置効果 = 1.0 – 0.125 = 0.875
→ 奨学金の有無によって、進学率が87.5ポイント上昇した と解釈できる。
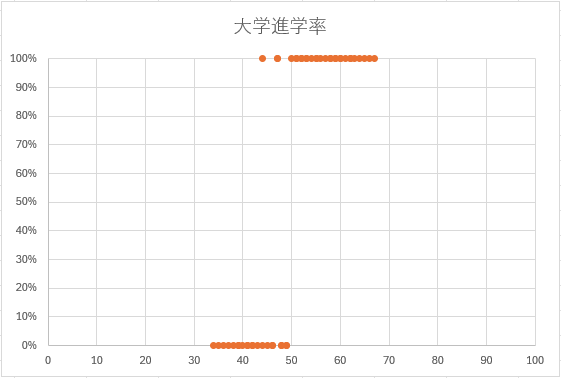
散布図で可視化
「得点X」を横軸、「進学率Y」を縦軸にプロットして散布図を作成します。
50 点を境に進学率がジャンプしていれば、処置効果が視覚的に確認できたことになます。
今回は以上となります。
ブックマークのすすめ
「ほわほわぶろぐ」を常に検索するのが面倒だという方はブックマークをお勧めします。ブックマークの設定は別記事にて掲載しています。

「お気に入り」の登録・削除方法【Google Chrome / Microsoft Edge】「お気に入り」の登録・削除方法【Google Chrome / Microsoft Edge】について解説している記事です。削除方法も掲載しています。...
【パソコン選び】失敗しないための重要ポイント | 現役エンジニア&プログラミングスクール講師【パソコン選び】失敗しないための重要ポイントについての記事です。パソコンのタイプと購入時に検討すべき点・家電量販店で見かけるCPUの見方・購入者が必要とするメモリ容量・HDDとSSDについて・ディスプレイの種類・バッテリーの持ち時間や保証・Officeソフト・ウィルス対策ソフトについて書いています。...
準実験:回帰不連続デザイン(RDD)-1280x720.jpg)

帰無仮説と対立仮設・有意水準・P値・z検定-640x360.png)
MMMと準実験-640x360.jpg)
ロジスティック回帰・決定木-640x360.jpg)
-640x360.jpg)
準実験:差分の差分法-640x360.jpg)
データドリブンマーケティング-と-マーケティングミックスモデリング(MMM)-640x360.jpg)

カスタム調査とシンジケートデータ-320x180.png)
帰無仮説と対立仮設・有意水準・P値・z検定-320x180.png)
準実験:合成コントロール法-320x180.jpg)
準実験:回帰不連続デザイン(RDD)-320x180.jpg)
準実験:傾向スコアマッチング(PSM)-320x180.jpg)