目標
「ロジスティック回帰、決定木」について理解する
ロジスティック回帰（Logistic Regression）
手法の概要
- 二値分類（0/1） の予測に使う統計モデル。
- 入力変数（説明変数）と目的変数の関係を「確率」としてモデル化する。
- 出力は 0〜1の確率 → しきい値を設定してクラス分類。
数式イメージ：
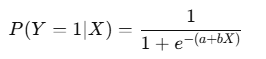
利用方法
- 「Yes/No」「成功/失敗」「購入する/しない」など、結果が二値の問題。
- 係数を見れば「どの要因が結果にどう影響しているか」が解釈できる。
具体的な用途事例
- 医療: 患者が「病気を発症するか/しないか」。
- マーケティング: 顧客が「購入するか/しないか」を予測。
- 金融: 申込者が「ローン返済を延滞するか/しないか」。
Excelでロジスティック回帰を実行する簡単な例
例題
顧客が「広告クリックしたか（X）」と「購入したか（Y）」のデータを利用して「クリックと購入の関係性」「購入確率の数値化」「効果の強さを「オッズ比」で表現」「データの適合度（どのくらい当たっているか）」を確認します。この確認に「対数尤度」を利用します。
次のような二値分類「0/1」で扱うデータを準備します。
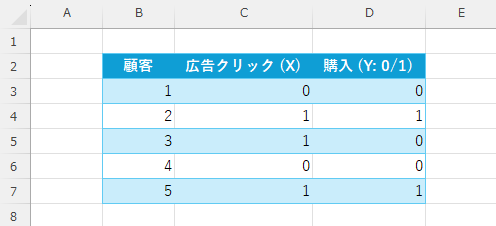
適当なセルに「切片」と「係数」の欄を作成し、初期値を「0」とします。その他にE列に「予測確率」の欄も作成し、数式「=1/(1+EXP(-( $C$10 + $C$11*C3 )))」を入力しE7までコピーします。
=1/(1+EXP(-( $C$10 + $C$11*C3 )))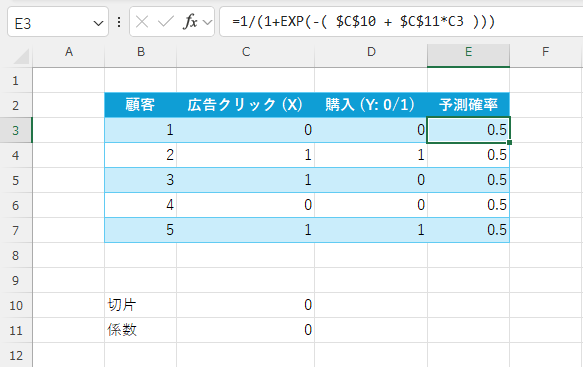
F列に「各行の対数尤度」を計算すします（数式：YがD列、予測PがE列の場合）。
=D3*LN(E3) + (1-D3)*LN(1-E3)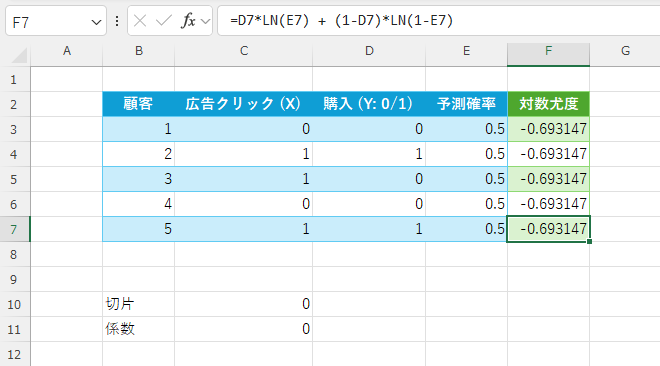
C12に対数尤度の合計を出力
=SUM(F3:F7)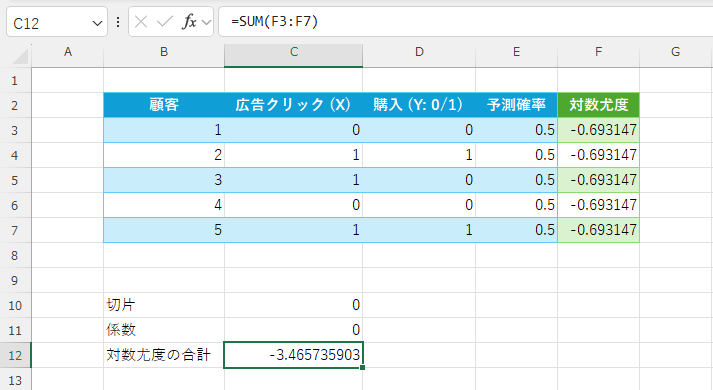
この後は、ソルバーで C10（係数）・C11（切片）を動かして、合計対数尤度（C12）が −3.4657 より大きく（＝0に近づく） なるよう最適化するように処理します。
ソルバーの利用
- データ → ソルバー を開く。
- 「目的セル」= $C$12（対数尤度合計）。
- 「目的」= 最大化。
- 「変数セル」= $C$10:$C$11（切片と係数）。
- 制約のない変数を非負数にするのチェックを外す。（※注意：後述）
- 解法方法 = GRG 非線形 を選択。
- 実行。
「データ」タブをクリック
「ソルバー」をクリック
各値の設定して「解決」をクリック
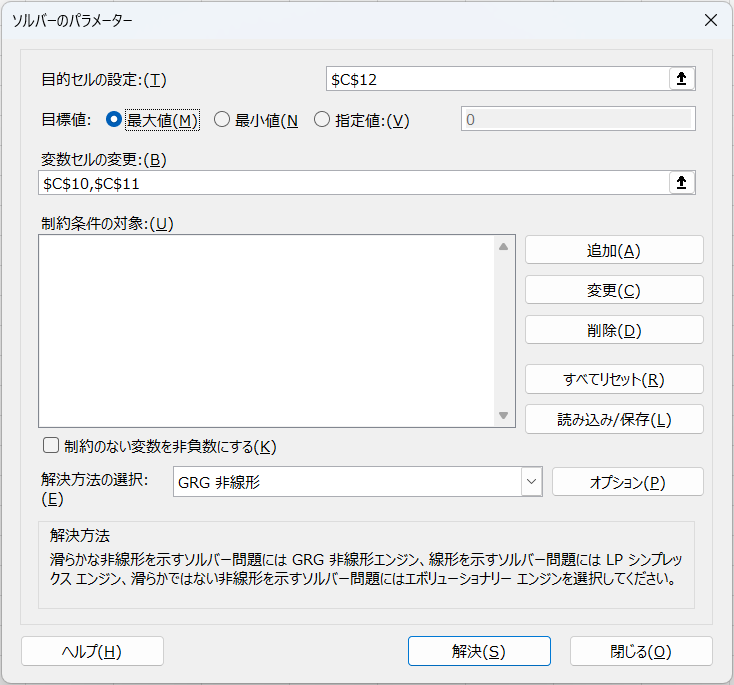
係数が算出されます。
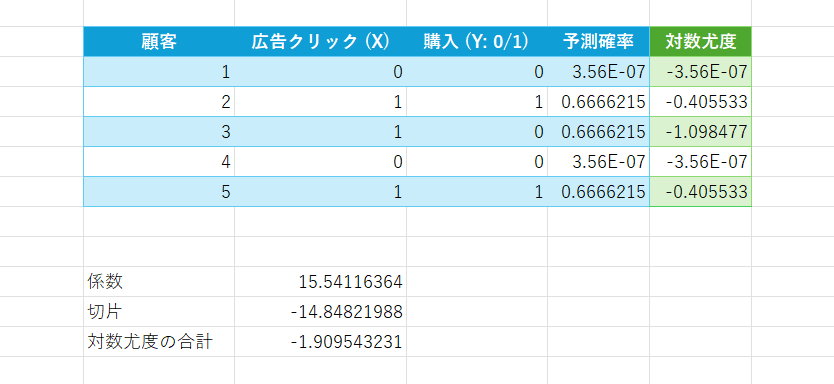
出力から分かったこと
クリックと購入の関係性
- 係数 b がプラスになる → 「広告をクリックした人ほど購入する確率が高い」
- 切片 a がマイナスになる → 「クリックしない人は購入する確率が非常に低い」
購入確率を数値化
推定結果（例：正則化なしの理論解）
- X=0 → P≈0（クリックなしではほぼ買わない）
- X=1 → P≈0.667（クリックしたら約67%が購入）
効果の強さを「オッズ比」で表現できる
- 係数 b を指数化するとオッズ比が分かります。
- b が大きければ「クリックした人は何倍も買いやすい」と言える。
データの適合度（どのくらい当たっているか）
- 対数尤度の合計が −3.465 → −1.909 に改善し、モデルが「当たりやすくなった」
決定木（Decision Tree）
手法の概要
- データを「もし〜なら〜」というルールに基づいて分岐させ、分類や回帰を行うアルゴリズム。
- 木構造で分岐していくので、直感的にわかりやすい。
例：もし「年齢 < 30」かつ「Web広告クリックあり」なら → 購入
それ以外なら → 未購入
利用方法
- 目的変数が カテゴリ（○○か△△か、などの確立や分類結果を扱う） の場合
- → 分類木（classification tree）
- 目的変数が 数値（売上金額・購入金額などの連続する値） の場合
- → 回帰木（regression tree）
- 単純な解釈がしやすく、特徴量の重要度もわかる。
具体的な用途事例
- マーケティング: 顧客の属性や行動から「どんな人が購入するか」をルール化。
- 教育: 学習時間・宿題提出率から「合格/不合格」を予測。
- 医療: 患者データから「手術成功率」を予測。
- 業務改善: クレームが「重大化する/しない」要因を特定。
決定木（顧客購買予測の例の分類木）
例えば「年齢」「広告クリック」「年収」で顧客の購入を予測するシナリオ。
┌── 広告クリック = なし ──→ 購入しない確率高い
│
開始 ─ 年齢 < 30 ┤
│
└── 広告クリック = あり ──→ 年収で分岐
│
├── 年収 < 400万 → 購入確率 40%
└── 年収 ≥ 400万 → 購入確率 75%このように「もし〜なら〜」の形でルール化されるので、顧客セグメント別に購買傾向を理解するのに役立ちます。
ロジスティック回帰 vs 決定木
| 観点 | ロジスティック回帰 | 決定木 |
|---|---|---|
| 出力 | 確率（0〜1） | クラス or 数値 |
| 解釈性 | 係数で「要因の影響度」が分かる | ルール形式で直感的に分かる |
| データの前提 | 線形性がある方が適合しやすい | 線形性は不要（複雑な境界も表現可能） |
| 強み | 統計的に安定、シンプル | 複雑な関係を捉えやすい |
| 弱み | 非線形関係は苦手 | 過学習しやすい（ランダムフォレスト等で改善） |
まとめ
ロジスティック回帰: 二値の確率を予測、係数の解釈がしやすい。
→ 例：顧客が購入する確率は？
決定木: 「もし〜なら〜」のルールで分類、直感的で非線形も扱える。
→ 例：どんな条件の顧客が購入するか？
今回は以上となります。
ブックマークのすすめ
「ほわほわぶろぐ」を常に検索するのが面倒だという方はブックマークをお勧めします。ブックマークの設定は別記事にて掲載しています。
