データサイエンス（Part.6）｜データ分析のプロセス３（t検定・ANOVA）
目次
目標
t検定について理解する
ANOVAについて理解する
t検定（t-test）
手法の概要
- 2つのグループの平均値に差があるかどうかを統計的に検証する手法。
- 「差が偶然ではなく、統計的に有意か？」を確認できる。
- データが正規分布に従うと仮定して用いられる。
主な種類
対応のないt検定（独立2標本 t検定）
- 別々の集団を比較する 検定。
- 「Aグループの平均」と「Bグループの平均」を比べたいときに使います。
- データの間には関連がありません。
- 例１： 男性と女性の「平均購入額」の比較（それぞれ別の人たち）。
- 例２： 東京の顧客と大阪の顧客の平均購入額の比較。
- 例３： 広告Aを見た人と広告Bを見た人の購入率比較。
- 👉 集団が完全に別なので「独立している」と言います。
対応のあるt検定（対応あり t検定）
- 同じ対象を2回測る（ペアになっている） データを比較する検定。
- 「前と後」や「条件Aと条件B」など、同一対象を比較するので「対応あり」。
- 例１：同じ顧客の「キャンペーン前とキャンペーン後」の購入額。
- 例２：同じ学生の「授業前テスト」と「授業後テスト」の点数。
- 例３：同じ患者の「投薬前の血圧」と「投薬後の血圧」。
- 👉 同じ人を2回測るので、「差分（後−前）」を1つのデータとして扱えるのがポイントです。
1標本t検定
- 1つのグループの平均 が「基準値」と違うかどうかを検定。
- 例１：ある商品の平均レビューが「3点（業界標準）」と異なるか。
- 例２：社員の平均残業時間が「月30時間」という基準より多いか少ないか。
- 👉 比較相手は「もう1つのグループ」ではなく「理論的な基準値」。
利用方法
- 2つのグループの平均を比較したいとき。
- サンプルサイズが比較的小さい場合（n<30程度でも使える）。
具体的な用途事例
- マーケティング: A/Bテストで「広告Aと広告Bでクリック率に差があるか」を検証。
- 教育: 新しい教材導入前後で、学習者のテスト点数が上がったかどうか。
- 医療: 新薬投与群とプラセボ群で平均血圧に差があるか。
Excelを利用したt検定
方法1: 関数を使う（次回ここから）
T.TEST 関数を使う（Excel 2010以降）
=T.TEST(配列1, 配列2, 尾, 型)- 配列1, 配列2：比較する2つのデータ範囲
- 尾：1（片側検定）または 2（両側検定）
- 型：
- 1 = 対応のある t検定
- 2 = 等分散を仮定した2標本 t検定
- 3 = 不等分散を仮定した2標本 t検定
分散分析（ANOVA: Analysis of Variance）
手法の概要
- 3つ以上のグループの平均値に差があるかを検証する方法。
- 「各グループ間の差」 と 「グループ内のばらつき」を比較して、統計的に有意か判断。
主な種類
一元配置分散分析（One-way ANOVA）
- 1つの要因（カテゴリ変数） がグループを分けている場合に、平均の差を比較する方法。
- t検定の「3グループ以上版」とイメージすると理解しやすいです。
- 例：広告媒体（TV、Web、新聞）の違いで売上に差があるか。
- グループ1 = TV広告を見た人の売上
- グループ2 = Web広告を見た人の売上
- グループ3 = 新聞広告を見た人の売上
→ 3つのグループの「平均売上」が同じかどうかを比べる。
- 👉 「1つの軸（広告媒体）」でグループ分けするから「一元」です。
二元配置分散分析（Two-way ANOVA）
- 2つの要因 がデータに影響しているときに使う方法。
- 要因ごとの効果だけでなく、組み合わせ（交互作用）の効果が検証できます。
- 例：広告媒体（TV、Web、新聞） × 地域（東京、大阪）の組み合わせで売上に差があるか。
- →TV広告 × 東京
- →TV広告 × 大阪
- →Web広告 × 東京
- →Web広告 × 大阪
- →新聞広告 × 東京
- →新聞広告 × 大阪
- → 「広告媒体の効果」「地域の効果」「広告媒体 × 地域の相互作用」を検証できる。
- 例：広告媒体（TV、Web、新聞） × 地域（東京、大阪）の組み合わせで売上に差があるか。
- 👉 「2つの軸（広告媒体と地域）」があるから「二元」です。
繰り返し測定ANOVA
- 同じ対象を複数回測定 したときに使う方法です。（同じ被験者を複数の条件下で測定した場合の差を検証。）
- 対応のあるt検定の「3条件以上版」とイメージするとわかりやすいです。
- 例：同じ被験者が「広告なし」「Web広告あり」「TV広告あり」の3条件下で購買意欲を測定。
- 同じ患者の血圧を「薬なし」「薬A」「薬B」で測定して比較。
- 例：同じ被験者が「広告なし」「Web広告あり」「TV広告あり」の3条件下で購買意欲を測定。
- 👉 同じ人を何度も測るので、「個人差」を除いた上で「条件の違いによる平均差」を検証できます。
利用方法
- 比較したいグループが 3つ以上ある場合。
- グループ間の違いだけでなく、「要因間の交互作用（相互効果）」も調べたい場合。
具体的な用途事例
- マーケティング: 価格帯（低価格・中価格・高価格）の違いが売上に影響するか。
- 製造業: 製造条件（温度・圧力・機械種類）が製品品質に与える影響を検証。
- 心理学: 学習法（映像・テキスト・グループ学習）によるテストスコアの差。
Excelを利用したANOVA
データ分析ツールを使う
- メニュー「データ」 → 「データ分析」 → 「分散分析: 一元配置」または「分散分析: 二元配置」
- データ範囲を指定（例: 各列がグループを表すように入力）。
- 出力先を指定すると、分散分析表（ANOVA表） が出力されます。
例：三名の生徒のある科目の平均点に有意差はあるか？
（分散分析：一元配置）
「データ」タブをクリック
分析ツールをクリック
「分散分析: 一元配置」を選択して「OK」をクリック
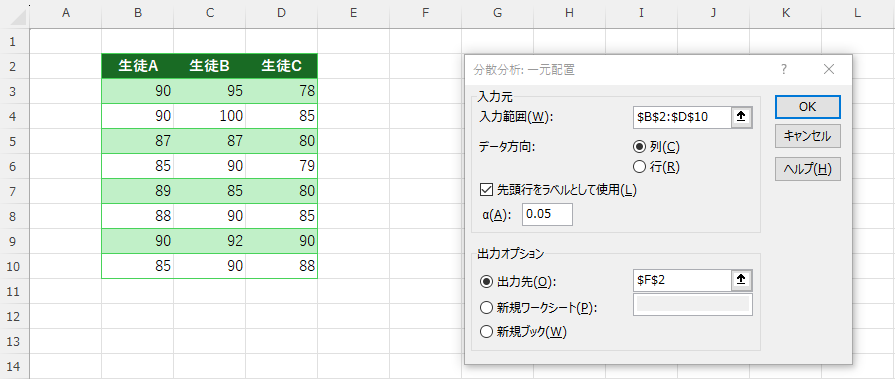
入力範囲を選択し、一覧表の先頭行をラベル（項目名）として使用するかを確認し必要ならチャックを入れます。出力先も指定があれば指定します。
出力結果
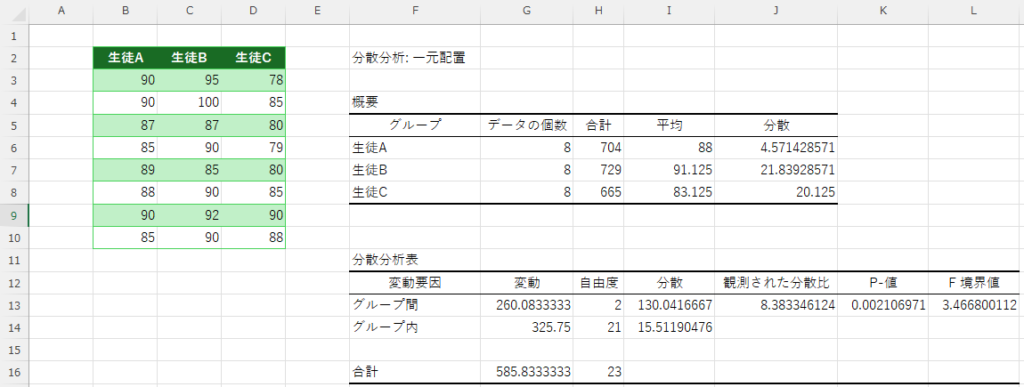
出力の見方
- p値（P-value） が 0.05 未満なら、グループ（生徒）間に有意な差がある。
例：三名の生徒の三科目の平均点に有意差はあるか？
（分散分析：繰り返えしのある二元配置）
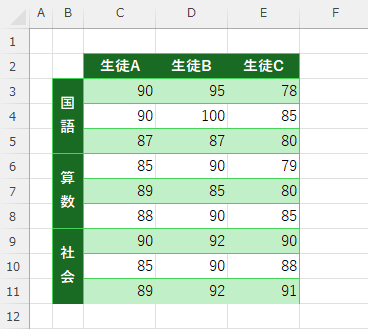
「データ」タブをクリック
分析ツールをクリック
「分散分析: 繰り返しのある二元配置」を選択して「OK」をクリック
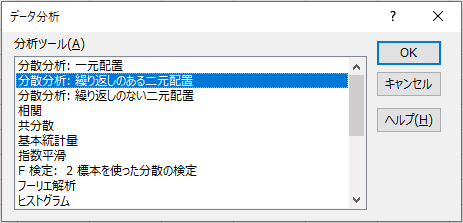
入力範囲を選択（ラベルを含んで選択）し、1標本当たりの行数を入力します。この場合は国語が3行、算数が3行、社会が3行なので「3」と入力します。出力先も指定があれば指定します。
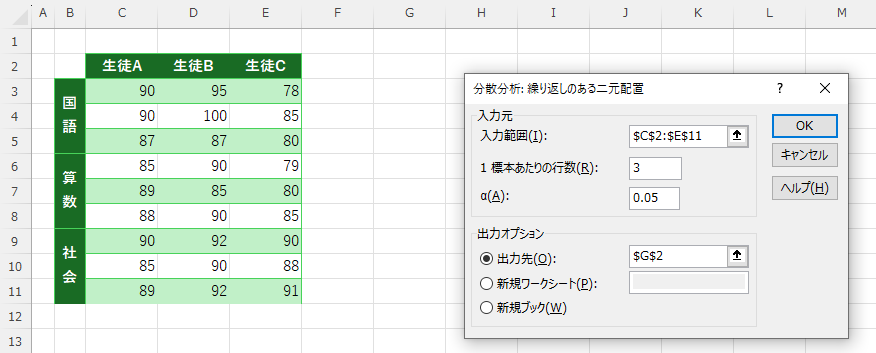
出力結果
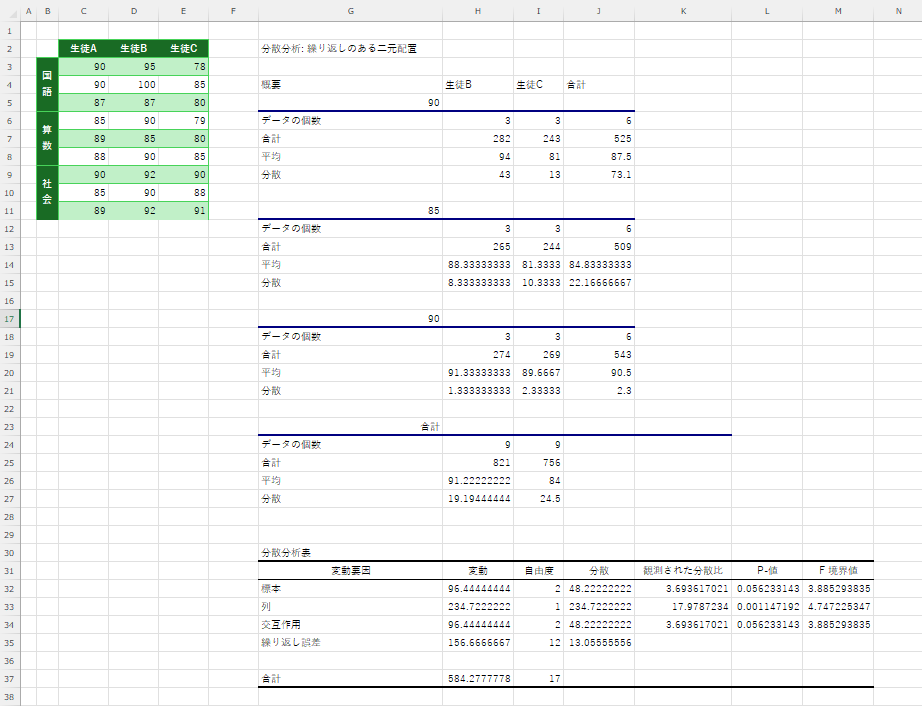
出力の見方
- p値（P-value） が 0.05 未満なら、グループ間に有意な差がある。
- 標本（教科間）としては有意な差は無い
- 列（生徒間）では有意な差はある
- 交互作用「教科」と「生徒」の組み合わせでは有意な差はない
例：三名の生徒の三科目の平均点に有意差はあるか？
（分散分析：繰り返えしのない二元配置）
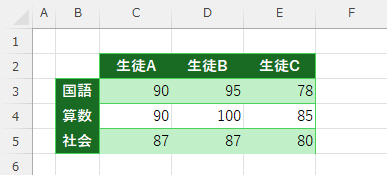
「データ」タブをクリック
分析ツールをクリック
「分散分析: 繰り返しのない二元配置」を選択して「OK」をクリック
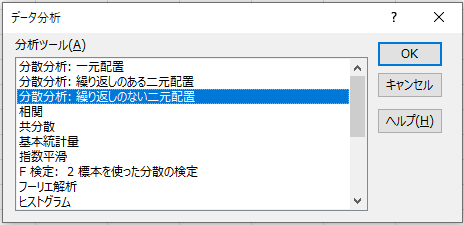
入力範囲を選択（ラベルを含んだ場合はラベルにチェック）し、出力先も指定があれば指定します。
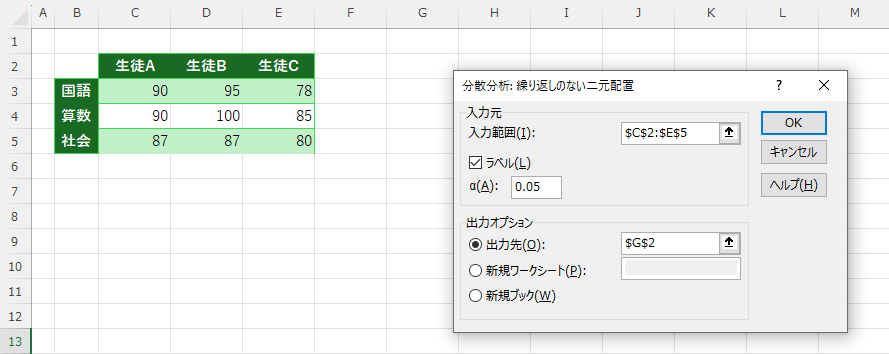
出力結果
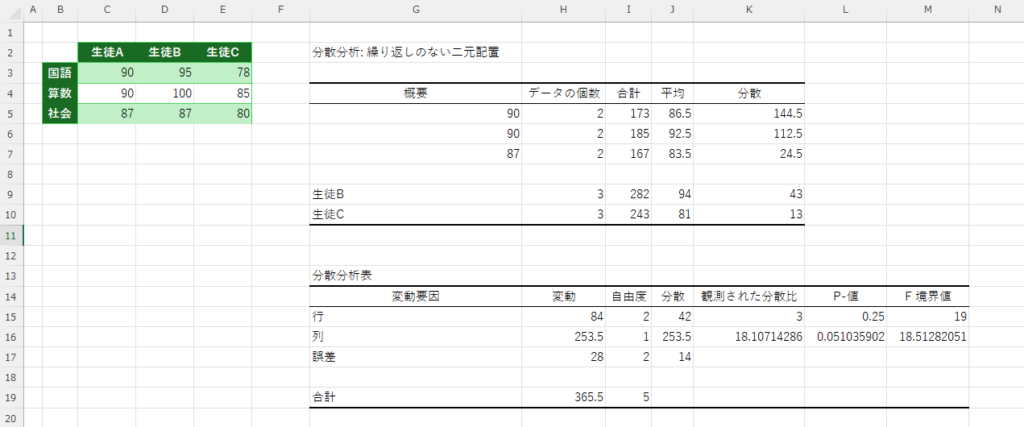
出力の見方
- p値（P-value） が 0.05 未満なら、グループ間に有意な差がある。
- 行（教科間）としては有意な差は無い
- 列（生徒間）では有意な差はある
t検定とANOVAの関係
- t検定 → 2グループ間の平均の差を検定。
- ANOVA → 3グループ以上の平均の差を一度に検定できる。
- ANOVAはt検定の拡張版 と考えられる。
- 例えば3グループを比較したいときに、t検定を複数回やると誤検出（多重比較の問題）が増えるため、ANOVAを使う。
まとめ
どちらも「平均値の差が偶然ではないか」を検証する手法で、A/Bテストや施策効果測定に頻繁に使われる。
- t検定 = 2グループ比較（AとBに差があるか？）
- ANOVA = 3グループ以上比較（A・B・Cで差があるか？ 要因の組み合わせで違うか？）
今回は以上となります。
ブックマークのすすめ
「ほわほわぶろぐ」を常に検索するのが面倒だという方はブックマークをお勧めします。ブックマークの設定は別記事にて掲載しています。
「お気に入り」の登録・削除方法【Google Chrome / Microsoft Edge】「お気に入り」の登録・削除方法【Google Chrome / Microsoft Edge】について解説している記事です。削除方法も掲載しています。...
【パソコン選び】失敗しないための重要ポイント | 現役エンジニア&プログラミングスクール講師【パソコン選び】失敗しないための重要ポイントについての記事です。パソコンのタイプと購入時に検討すべき点・家電量販店で見かけるCPUの見方・購入者が必要とするメモリ容量・HDDとSSDについて・ディスプレイの種類・バッテリーの持ち時間や保証・Officeソフト・ウィルス対策ソフトについて書いています。...
