目標
（pythonの）「集合」に対して様々な判定方法を理解し利用できる。
- 「演算子 == 」「演算子 != 」を利用した等価性判定
- 「in」「not in」を利用した帰属性判定
- 「isdisjointメソッド」を利用した素の判定
- 「演算子 <= 」「issubsetメソッド」を利用した部分集合の判定
- 「演算子 < 」を利用した真部分集合の判定
- 「演算子 >= 」「issupersetメソッド」を利用した超集合の判定
- 「演算子 > 」を利用した真超集合の判定
（pythonの）「集合」の操作方法
（pythonの）「集合」に対する様々な判定方法
「集合」は要素に順序や重複がないことに基づく、集合同士の様々な演算を行うことができます。具体的には以下の内容です。
- ふたつの集合が同様のものとする等価性の判定
- ある集合の中に、任意の値の存在を確認する帰属性の判定
- 比較する集合同士に共通の要素がないことを確認する素の判定
- 集合がある集合の一部である部分集合の判定
- 部分集合のうち真部分集合（等価でない部分集合）の判定
- 集合が他の集合を全て含んでいる超集合の判定
- 超集合のうち真超集合（等価でない超集合）の判定
「演算子 == 」「演算子 != 」を利用した等価性判定
等価性の判定とは、ある集合と、他の集合の要素が同じか、異なるかを判定します。
「演算子 == 」を利用する場合、比較する集合が等価であれば「True」、不等価であれば「False」を返します。
「演算子 != 」を利用する場合、比較する集合が等価であれば「False」、不等価であれば「True」を返します。
サンプルプログラム
set_sample_no1 = {1, 2, 3, 4, 5}
set_sample_no2 = {5, 3, 1, 4, 2}
set_sample_no3 = {1, 3, 5, 7, 9}
#「演算子 == 」は比較する集合が等価である場合「True」となります。
print(set_sample_no1 == set_sample_no2)
print(set_sample_no1 == set_sample_no3)
print('------------------------------')
#「演算子 != 」は比較する集合が等価である場合「False」となります。
#「!」は打消しの意味です。
print(set_sample_no1 != set_sample_no2)
print(set_sample_no1 != set_sample_no3)実行結果
「in」「not in」を利用した帰属性判定
帰属性の判定とは、ある集合の中に、任意の値が存在するか、しないかを判定します。
「in 演算子」では、指定する値が集合のなかに存在する場合「True」、存在しない場合「False」を返します。
「not in 演算子」では、指定する値が集合のなかに存在する場合「False」、存在しない場合「True」を返します。
サンプルプログラム
set_sample_no4 = {1, 2, 3, 4, 5}
#「in 演算子」では、指定する値が集合のなかに存在する場合「True」となります。
print(3 in set_sample_no4)
print(10 in set_sample_no4)
print('------------------------------')
#「not in 演算子」では、指定する値が集合のなかに存在する場合「False」となります。
print(3 not in set_sample_no4)
print(10 not in set_sample_no4)実行結果
「isdisjointメソッド」を利用した素の判定
素の判定とは、比較する集合同士に共通の要素があるか、ないかを判定します。
「isdisjoint メソッド」は比較する集合が素（共通の要素がない）の場合に「True」を返します。
サンプルプログラム
set_sample_no5 = {1, 3, 5, 7}
set_sample_no6 = {2, 4, 6, 8}
set_sample_no7 = {1, 2, 6, 8}
#「isdisjoint メソッド」は比較する集合が素（共通の要素がない）の場合に「True」を返します。
print(set_sample_no5.isdisjoint(set_sample_no6))
print('------------------------------')
# 比較する集合が素（共通の要素がない）でない場合は「False」を返します。
print(set_sample_no5.isdisjoint(set_sample_no7))実行結果
「演算子 <= 」「issubsetメソッド」を利用した部分集合の判定
「部分集合」とは「ある集合」の「一部の集合」であることをさします。
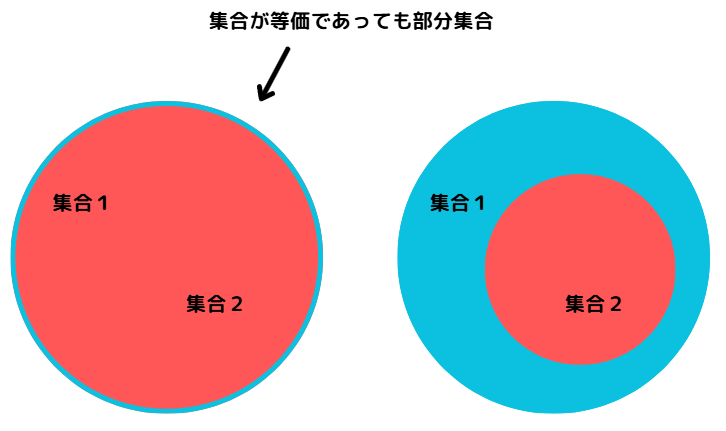
部分集合の判定は「演算子 <= 」や「issubsetメソッド」を利用します。「集合２」は「集合１」の部分集合かを判定する場合、次のように記述します。
集合２ <= 集合１
集合２.issubset(集合１)
サンプルプログラム
set_sample_no8 = {1, 3, 5, 7, 9}
set_sample_no9 = {1, 5, 7}
set_sample_no10 = {1, 5, 8}
#「集合２ <= 集合１」は「集合２」が「集合１」の部分集合の場合に「True」を返します。
print(set_sample_no9 <= set_sample_no8)
print(set_sample_no10 <= set_sample_no8)
print('------------------------------')
#「集合２.issubset(集合１)」は「集合２」が「集合１」の部分集合の場合に「True」を返します。
print(set_sample_no9.issubset(set_sample_no8))
print(set_sample_no10.issubset(set_sample_no8))実行結果
「演算子 < 」を利用した真部分集合の判定
「真部分集合」とは「部分集合」のうち「等価でない集合」であることをさします。
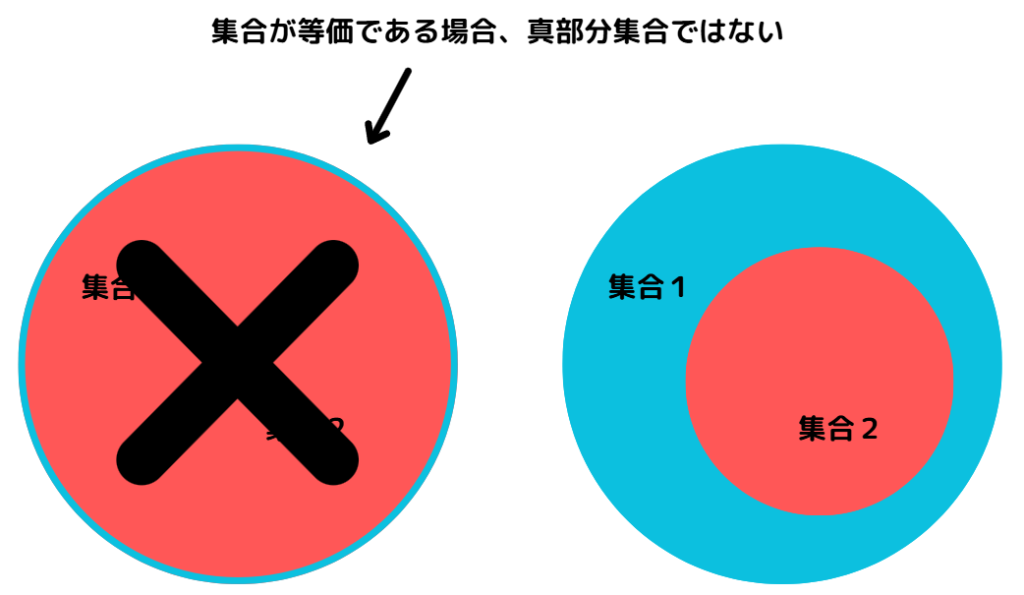
真部分集合の判定は「演算子 < 」を利用します。「集合２」は「集合１」の真部分集合かを判定する場合、次のように記述します。
集合２ < 集合１
サンプルプログラム
set_sample_no11 = {1, 3, 5, 7, 9}
set_sample_no12 = {1, 3, 5, 7, 9}
set_sample_no13 = {1, 3, 7, 9}
#「集合２ < 集合１」は「集合２」が「集合１」の真部分集合の場合に「True」を返します。
# 等価なので「False」となります（真部分集合でない）。
print(set_sample_no12 < set_sample_no11)
# 等価でないので「True」となります（真部分集合）。
print(set_sample_no13 < set_sample_no11)実行結果
「演算子 >= 」「issupersetメソッド」を利用した超集合の判定
「超集合」とは「集合」が「他の集合」を全て含んでいる集合のことです。
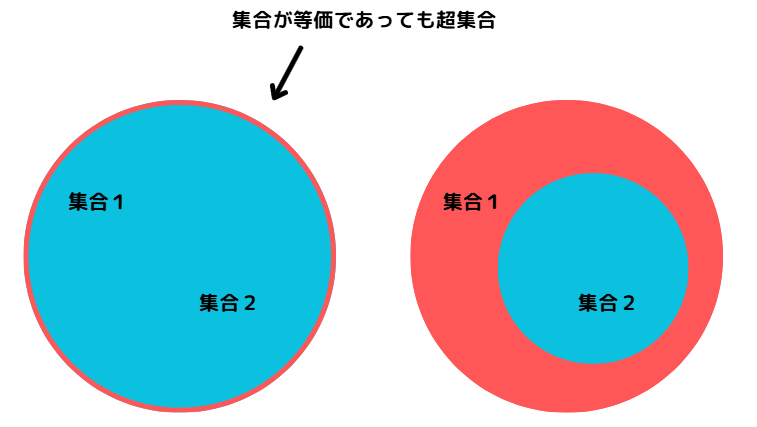
超集合の判定は「演算子 >= 」「issupersetメソッド」を利用します。「集合１」は「集合２」の超集合かを判定する場合、次のように記述します。
集合１ >= 集合２
集合１.issuperset(集合２)
サンプルプログラム
set_sample_no14 = {1, 3, 5, 7, 9}
set_sample_no15 = {1, 3, 5, 7, 9}
set_sample_no16 = {1, 5, 9}
set_sample_no17 = {1, 5, 8}
#「集合１>= 集合２」は「集合１」が「集合２」の超集合の場合に「True」を返します。
print(set_sample_no14 >= set_sample_no15)
print(set_sample_no14 >= set_sample_no16)
print(set_sample_no14 >= set_sample_no17)
print('------------------------------')
#「集合１.issuperset(集合２)」は「集合１」が「集合２」の超集合の場合に「True」を返します。
print(set_sample_no14.issuperset(set_sample_no15))
print(set_sample_no14.issuperset(set_sample_no16))
print(set_sample_no14.issuperset(set_sample_no17))実行結果
「演算子 > 」を利用した真超集合の判定
「真超集合」とは「超集合」のうち「等価でない集合」のことをさします。
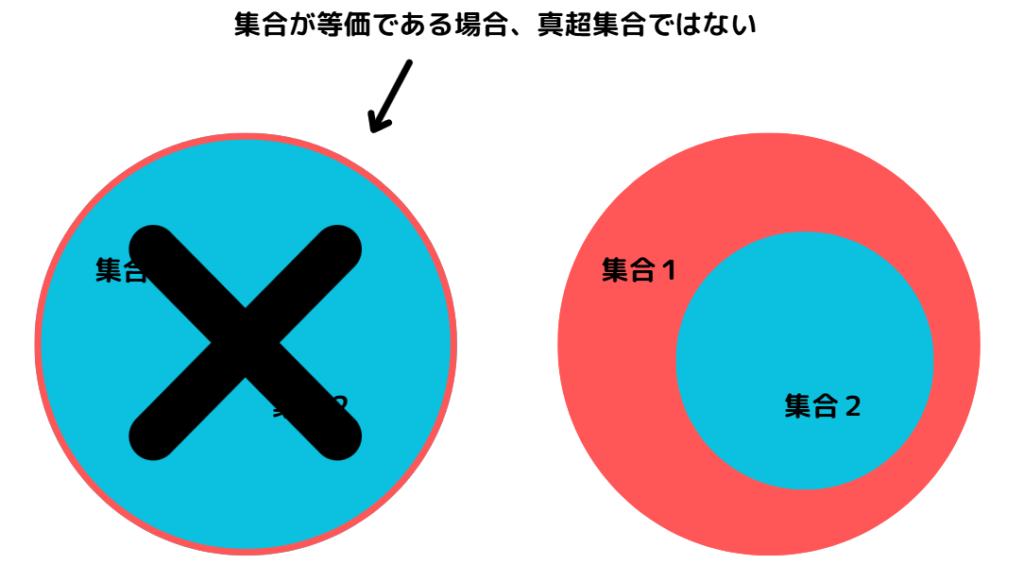
真超集合の判定は「演算子 > 」を利用します。「集合１」は「集合２」の真超集合かを判定する場合、次のように記述します。
集合１ > 集合２
サンプルプログラム
set_sample_no14 = {1, 3, 5, 7, 9}
set_sample_no15 = {1, 3, 5, 7, 9}
set_sample_no16 = {1, 5, 9}
set_sample_no17 = {1, 5, 8}
#「集合１ > 集合２」は「集合１」が「集合２」の真超集合の場合に「True」を返します。
print(set_sample_no14 > set_sample_no15 )
print(set_sample_no14 > set_sample_no16 )
print(set_sample_no14 > set_sample_no17 )実行結果
今回は以上になります。
ブックマークのすすめ
「ほわほわぶろぐ」を常に検索するのが面倒だという方はブックマークをお勧めします。ブックマークの設定は別記事にて掲載しています。
