05-Python

Python（Part.43）｜ python【集合（利用編-3）】【複数の集合に対する様々な要素の取り出し】

 
python｜ まとめ　| 現役エンジニア&プログラミングスクール講師「python」のまとめページです。pythonに関して抑えておきたい知識や文法やにについて記事をまとめています。まとめページの下部には「おすすめの学習書籍」「おすすめのITスクール情報」「おすすめ求人サイト」について情報を掲載中...
目次
  1. 目標
  2. 「複数の集合」に対して様々な要素の取り出し方法
  3. ブックマークのすすめ

目標

複数の集合に対して様々な要素の取り出し方法を理解し利用できる。

  • 「演算子 | 」や「unionメソッド」を利用した和集合の取り出し
  • 「演算子 & 」や「intersectionメソッド」を利用した積集合の取り出し
  • 「演算子 – 」や「differenceメソッド」を利用した差集合の取り出し
  • 「演算子 ^ 」を利用した対称差集合の取り出し

「複数の集合」に対して様々な要素の取り出し方法

「複数の集合」に対して様々な要素の取り出し方法

「集合」は「他の集合」と要素を比較し、「いずれかの集合に存在する要素」「いずれの集合にも存在する要素」「片方の集合にしかない要素」などのルールで新しい集合を取得することができます。具体的には以下の内容です。

  • いずれかの集合に存在する要素（和集合）
  • いずれの集合にも存在する共通の要素（積集合）
  • いずれかの集合のうち、一方の集合の要素を取り除いた集合（差集合）
  • 共通の要素を取り除いた集合（対象差集合）

「演算子 | 」や「unionメソッド」を利用した和集合の取り出し

和集合は、複数の集合の集まりのなかで、少なくともひとつの集合に含まれる要素を集めた集合のことです。ベン図では次の緑の範囲の要素をもつ集合となります。

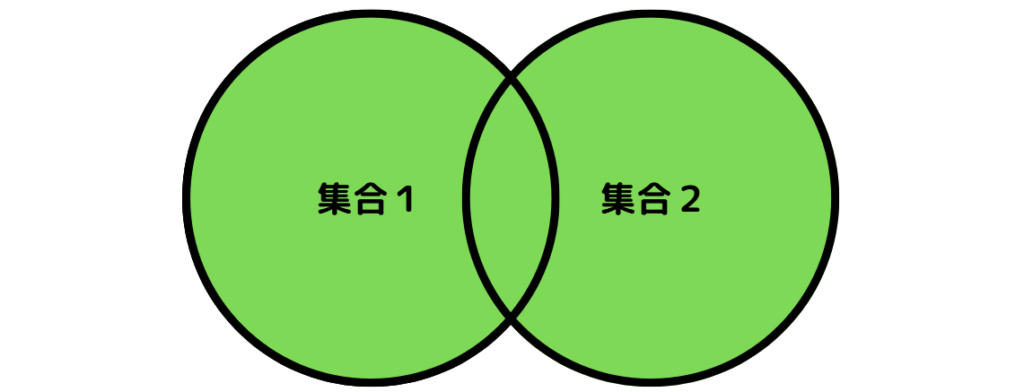
和集合は「演算子 | 」や「unionメソッド」を利用して求めることができます。

記号「|」はShiftキーを押しながら「\」を押下します。

サンプルプログラム

set_sample_no1 = {1, 2, 7, 9, 5}
set_sample_no2 = {5, 3, 8, 4, 2}

#「演算子 | 」を利用すると和集合を求めることができます。
print(set_sample_no1 | set_sample_no2)
print('------------------------------')
#「unionメソッド」を利用することでも和集合を求めることができます。
print(set_sample_no1.union(set_sample_no2))

実行結果

「演算子 | 」や「unionメソッド」は和集合を求めるために（演算結果は一時的な表示のみ）利用されます。このことから求めた和集合を再利用する場合は変数に紐づける必要があります。

新しい変数に紐づける場合は「代入式 = 」を利用しますが、既存の集合で利用している変数の紐づけを更新する場合には「演算子 |= 」や「updateメソッド」を利用します。

「演算子 |= 」や「updateメソッド」を利用した変数の更新

サンプルプログラム

set_sample_no1 = {1, 2, 7, 9, 5}
set_sample_no2 = {5, 3, 8, 4, 2}

#「演算子 |= 」を利用すると、既存の変数（|=の左側の変数）を、求めた和集合に更新できます。
set_sample_no1 |= set_sample_no2
print(set_sample_no1)
print('------------------------------')

set_sample_no1 = {1, 2, 7, 9, 5}
set_sample_no2 = {5, 3, 8, 4, 2}

#「updateメソッド」を利用すると、既存の変数を、求めた和集合に更新できます。
set_sample_no1.update(set_sample_no2)
print(set_sample_no1)
print('------------------------------')

#　既存の変数を、求めた和集合に更新せず、新しい変数を利用する場合は代入式を利用します。
set_sample_no1 = {1, 2, 7, 9, 5}
set_sample_no2 = {5, 3, 8, 4, 2}
set_sample_no3 = set_sample_no1.union(set_sample_no2)
print(set_sample_no1)
print(set_sample_no3)

実行結果

「演算子 &」や「intersectionメソッド」を利用した積集合の取り出し

積集合は、複数の集合の集まりのなかで、全ての集合に共通に含まれる要素を集めた集合のことです。ベン図では次の濃い緑の範囲の要素（重なっている部分）となります。

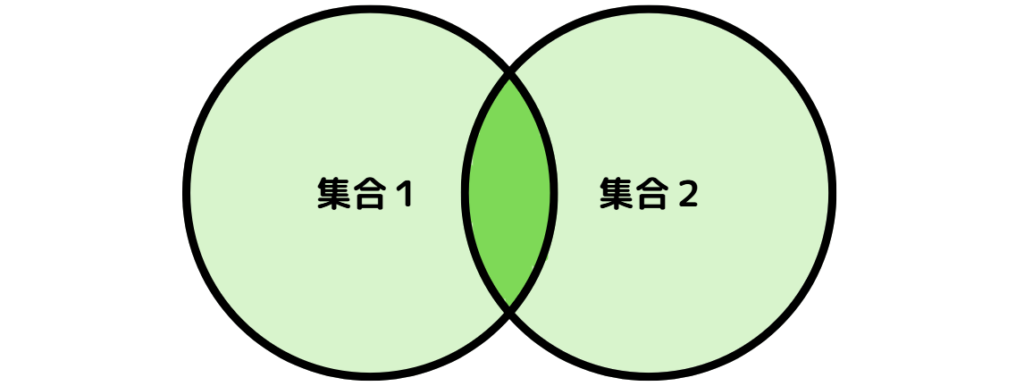
積集合は「演算子 &」や「intersectionメソッド」を利用して求めることができます。

記号「&」はShiftキーを押しながら「6」を押下します。

サンプルプログラム

set_sample_no1 = {1, 2, 7, 9, 5}
set_sample_no2 = {5, 3, 8, 4, 2}

#「演算子 & 」を利用すると積集合を求めることができます。
print(set_sample_no1 & set_sample_no2)
print('------------------------------')
#「intersectionメソッド」を利用することでも積集合を求めることができます。
print(set_sample_no1.intersection(set_sample_no2))

実行結果

「演算子 & 」や「intersectionメソッド」は積集合を求めるために（演算結果は一時的な表示のみ）利用されます。このことから求めた積集合を再利用する場合は変数に紐づける必要があります。

新しい変数に紐づける場合は「代入式 = 」を利用しますが、既存の集合で利用している変数の紐づけを更新する場合には「演算子 &= 」や「intersection_updateメソッド」を利用します。

「演算子 &=」や「intersection_updateメソッド」を利用した変数の更新

サンプルプログラム

set_sample_no1 = {1, 2, 7, 9, 5}
set_sample_no2 = {5, 3, 8, 4, 2}

#「演算子 &= 」を利用すると、既存の変数（&=の左側の変数）を、求めた積集合に更新できます。
set_sample_no1 &= set_sample_no2
print(set_sample_no1)
print('------------------------------')

set_sample_no1 = {1, 2, 7, 9, 5}
set_sample_no2 = {5, 3, 8, 4, 2}

#「intersection_updateメソッド」を利用すると、既存の変数を、求めた積集合に更新できます。
set_sample_no1.intersection_update(set_sample_no2)
print(set_sample_no1)
print('------------------------------')

#　既存の変数を、求めた積集合に更新せず、新しい変数を利用する場合は代入式を利用します。
set_sample_no1 = {1, 2, 7, 9, 5}
set_sample_no2 = {5, 3, 8, 4, 2}
set_sample_no3 = set_sample_no1.intersection(set_sample_no2)
print(set_sample_no1)
print(set_sample_no3)

実行結果

「演算子 – 」や「difference メソッド」を利用した差集合の取り出し

差集合は、複数の集合の集まりのなかで、「ある集合」のうち、他の集合に含まれる要素を除いた集合のことです。ベン図では次の緑の範囲の要素となります。

集合１-集合２の場合

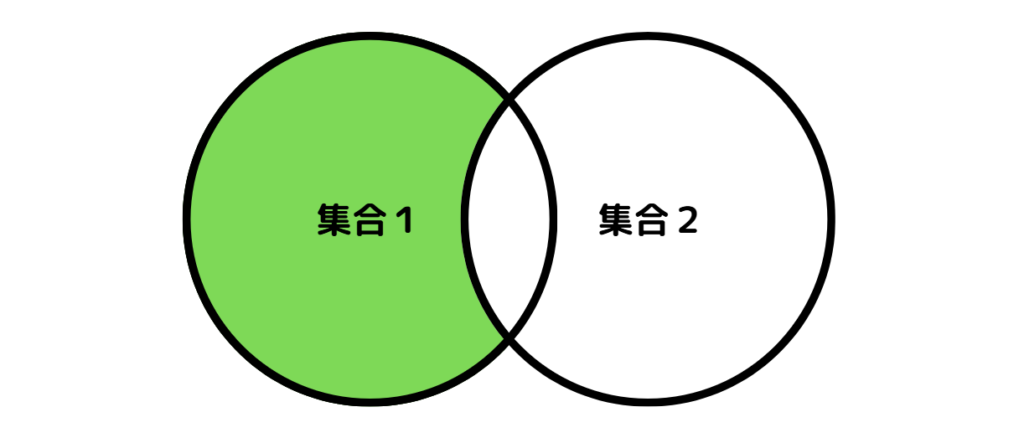
集合２-集合１の場合

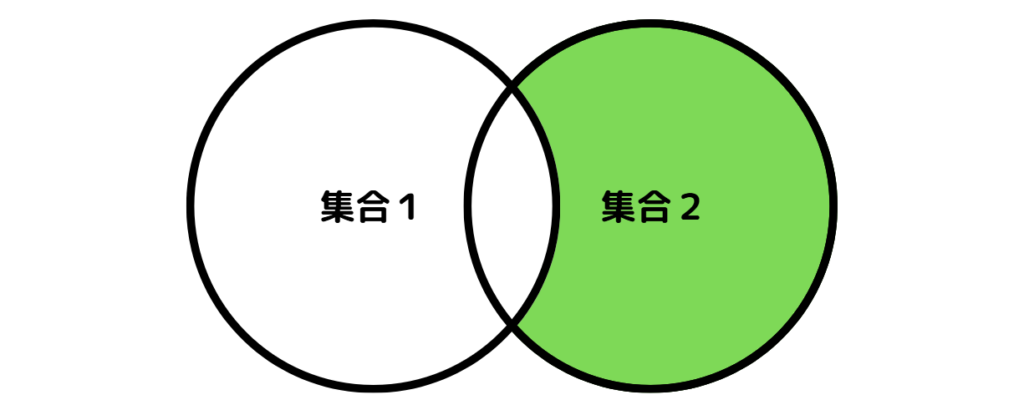
差集合は「演算子 – 」や「differenceメソッド」を利用して求めることができます。

サンプルプログラム

set_sample_no1 = {1, 2, 7, 9, 5}
set_sample_no2 = {5, 3, 8, 4, 2}

#「演算子 - 」を利用すると差集合を求めることができます。
print('集合１ - 集合２',set_sample_no1 - set_sample_no2)
print('集合２ - 集合１',set_sample_no2 - set_sample_no1)
print('------------------------------')
#「differenceメソッド」を利用することでも差集合を求めることができます。
print('集合１ - 集合２',set_sample_no1.difference(set_sample_no2))
print('集合２ - 集合１',set_sample_no2.difference(set_sample_no1))

実行結果

「演算子 – 」や「differenceメソッド」は差集合を求めるために（演算結果は一時的な表示のみ）利用されます。このことから求めた差集合を再利用する場合は変数に紐づける必要があります。

新しい変数に紐づける場合は「代入式 = 」を利用しますが、既存の集合で利用している変数の紐づけを更新する場合には「演算子 -= 」や「difference_updateメソッド」を利用します。

「演算子 -= 」や「difference_updateメソッド」を利用した変数の更新

サンプルプログラム

set_sample_no1 = {1, 2, 7, 9, 5}
set_sample_no2 = {5, 3, 8, 4, 2}

#「演算子 -= 」を利用すると、既存の変数（-=の左側の変数）を、求めた差集合に更新できます。
set_sample_no1 -= set_sample_no2
print(set_sample_no1)
print('------------------------------')

set_sample_no1 = {1, 2, 7, 9, 5}
set_sample_no2 = {5, 3, 8, 4, 2}

#「difference_updateメソッド」を利用すると、既存の変数を、求めた差集合に更新できます。
set_sample_no1.difference_update(set_sample_no2)
print(set_sample_no1)
print('------------------------------')

#　既存の変数を、求めた差集合に更新せず、新しい変数を利用する場合は代入式を利用します。
set_sample_no1 = {1, 2, 7, 9, 5}
set_sample_no2 = {5, 3, 8, 4, 2}
set_sample_no3 = set_sample_no1.difference(set_sample_no2)
print(set_sample_no1)
print(set_sample_no3)

実行結果

「演算子 ＾」や「symmetric_differenceメソッド」を利用した対称差集合の取り出し

対称差集合は、複数の集合の集まりのなかで、共通している要素を含めない集合のことです。ベン図では次の緑の範囲の要素となります。

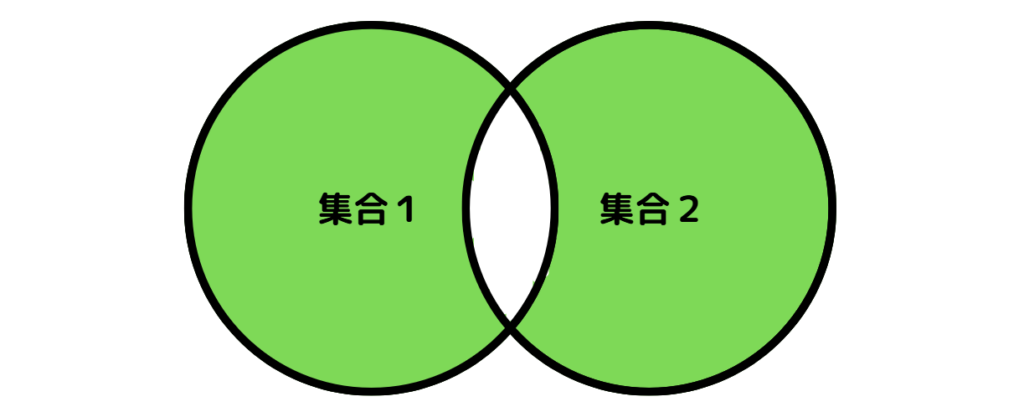
対称差集合は「演算子 ＾」や「symmetric_differenceメソッド」を利用して求めることができます。

サンプルプログラム

set_sample_no1 = {1, 2, 7, 9, 5}
set_sample_no2 = {5, 3, 8, 4, 2}

#「演算子 ^ 」を利用すると対称差集合を求めることができます。
print('対称差集合',set_sample_no1 ^ set_sample_no2)
print('------------------------------')
#「symmetric_differenceメソッド」を利用することでも対称差集合を求めることができます。
print('対称差集合',set_sample_no1.symmetric_difference(set_sample_no2))

実行結果

「演算子 ＾」や「symmetric_differenceメソッド」は対称差集合を求めるために（演算結果は一時的な表示のみ）利用されます。このことから求めた対称差集合を再利用する場合は変数に紐づける必要があります。

新しい変数に紐づける場合は「代入式 = 」を利用しますが、既存の集合で利用している変数の紐づけを更新する場合には「演算子 ^= 」や「symmetric_difference_updateメソッド」を利用します。

「演算子 ^= 」や「symmetric_difference_updateメソッド」を利用した変数の更新

サンプルプログラム

set_sample_no1 = {1, 2, 7, 9, 5}
set_sample_no2 = {5, 3, 8, 4, 2}

#「演算子 ^= 」を利用すると、既存の変数（^=の左側の変数）を、求めた対称差集合に更新できます。
set_sample_no1 ^= set_sample_no2
print(set_sample_no1)
print('------------------------------')

set_sample_no1 = {1, 2, 7, 9, 5}
set_sample_no2 = {5, 3, 8, 4, 2}

#「symmetric_difference_updateメソッド」を利用すると、既存の変数を、求めた対称差集合に更新できます。
set_sample_no1.symmetric_difference_update(set_sample_no2)
print(set_sample_no1)
print('------------------------------')

#　既存の変数を、求めた対称差集合に更新せず、新しい変数を利用する場合は代入式を利用します。
set_sample_no1 = {1, 2, 7, 9, 5}
set_sample_no2 = {5, 3, 8, 4, 2}
set_sample_no3 = set_sample_no1.symmetric_difference(set_sample_no2)
print(set_sample_no1)
print(set_sample_no3)

実行結果

今回は以上になります。

前の記事へ

次の記事へ

「python」おすすめ書籍 ベスト３ | 現役エンジニア&プログラミングスクール講師「python」の学習でお勧めしたい書籍をご紹介しています。お勧めする理由としては、考え方、イメージなどを適切に捉えていること、「生のpython」に焦点をあてて解説をしている書籍であることなどが理由です。勿論、この他にも良い書籍はありますが、特に質の高かったものを選んで記事にしています。ページの下部には「おすすめのITスクール情報」「おすすめ求人サイト」について情報を掲載中。...

ブックマークのすすめ

「ほわほわぶろぐ」を常に検索するのが面倒だという方はブックマークをお勧めします。ブックマークの設定は別記事にて掲載しています。

「お気に入り」の登録・削除方法【Google Chrome / Microsoft Edge】「お気に入り」の登録・削除方法【Google Chrome / Microsoft Edge】について解説している記事です。削除方法も掲載しています。...
【パソコン選び】失敗しないための重要ポイント | 現役エンジニア&プログラミングスクール講師【パソコン選び】失敗しないための重要ポイントについての記事です。パソコンのタイプと購入時に検討すべき点・家電量販店で見かけるCPUの見方・購入者が必要とするメモリ容量・HDDとSSDについて・ディスプレイの種類・バッテリーの持ち時間や保証・Officeソフト・ウィルス対策ソフトについて書いています。...
ifferenceメソッド intersectionメソッド python symmetric_differenceメソッド unionメソッド メソッド 初心者 和集合 対象差集合 差集合 積集合 集合
RELATED POST